🔗 UVA-11175 From D to E and Back

tags: `圖論(Graph)` `矛盾法(Contradiction)`

C++ 範例程式碼已於 UVA、瘋狂程設(CPE) 上測試通過。

無法使用 Python ，會 TLE 。

題意

取一個具有 $n$ $n$ 個頂點和 $m$ $m$ 條邊的有向圖 $D$ $D$ ，可以依照以下方式將 $D$ $D$ 轉換成躺平圖(Lying graph) $E$ $E$ 。
- $E$ 中的每個頂點代表 $D$ 的一條邊。例如，如果 $D$ 有一條邊 $uv$ ，那麼 $E$ 將有一個名為 $uv$ 的頂點。
- 若 $D$ 中存在邊 $(u, v)$ 和 $(v, w)$ ，則 $E$ 中也會有一條從頂點 $uv$ 到頂點 $vw$ 的邊。
給定一個圖 $E$ ，確定 $E$ 是否可能是某個有向圖 $D$ 的躺平圖(Lying graph)

註：躺平圖(Lying graph) 也叫做 Line Graph ，是一種特殊的圖，其頂點代表原圖的邊，邊代表原圖中的邊之間是否有共同的頂點(即原圖中的邊是否相鄰)。

思路：圖論(Graph)、矛盾法(Contradiction)

首先來思考什麼樣的情況會導致無法構成躺平圖，先說結論，對於任意兩點 $i$ 和 $j$ ，若存在一點 $k_1$ 使得 $i$ 和 $j$ 都能到達 $k_1$ ；但又存在另一點 $k_2$ 使得 $i$ 和 $j$ 只有其中一個能到達 $k_2$ ，則無法構成躺平圖。
為方便說明，將圖 $D$ 上的邊表示為 $(st, ed)$ 的形式，其中 $st$ 和 $ed$ 分別代表起點和終點，圖 $E$ 上的點表示為 $sted$ 的形式。
對於圖 $E$ 中的任意兩點 $i$ 和 $j$ ，若存在一點 $k$ 使得 $i$ 和 $j$ 都能到達 $k$ ，則顯然 $i$ 和 $j$ 在圖 $D$ 中對應的邊，具有相同的 $ed$ ，即 $i$ 和 $j$ 有共同的終點。而若 $i$ 和 $j$ 只有其中一個能到達 $k$ ，則 $i$ 和 $j$ 在圖 $D$ 中對應的邊，具有不同的 $ed$ 。這兩種情況若同時存在，顯然產生矛盾，故無法構成躺平圖。
如下圖所示，顯然圖 $E$ 中少了一條 $(bc, ce)$ 的邊，因此無法構成躺平圖。

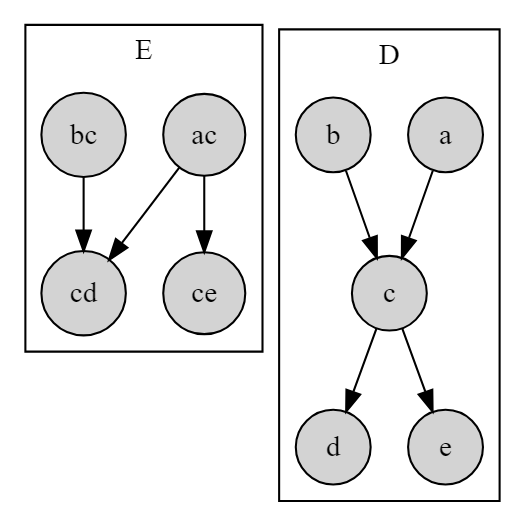
時間複雜度： $O(n^3)$
空間複雜度： $O(n^2)$

#include <bits/stdc++.h>
using namespace std;
const int N = 350;
#define endl '\n'

int main() {
    ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
    int t, kase=1, m, k, g[N][N], u, v;
    cin >> t;
    while (t--) {
        cin >> m >> k;
        memset(g, 0, sizeof(g));
        for (int i = 0; i < k; ++i) {
            cin >> u >> v;
            g[u][v] = 1;
        }
        bool flag = false;
        for (int i = 0; i < m && !flag; ++i) {
            for (int j = 0; j < m && !flag; ++j) {
                bool ck1 = false, ck2 = false;
                for (int k = 0; k < m && !flag; ++k) {
                    if (g[i][k] && g[j][k]) ck1 = true; // i 和 j 都能到達 k
                    if (g[i][k] != g[j][k]) ck2 = true; // i 和 j 只有其中一個能到達 k
                }
                if (ck1 && ck2) flag = true;
            }
        }
        cout << "Case #" << kase++ << ": " << (flag ? "No" : "Yes") << endl;
    }
    return 0;
}